Eells–Kuiper manifold
In mathematics, Eells–Kuiper manifold is a compactification of 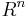 by an
by an 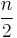 - sphere, where n = 2, 4, 8, or 16.
- sphere, where n = 2, 4, 8, or 16.
If n = 2, the Eells–Kuiper manifold is diffeomorphic to the real projective plane 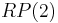 . For
. For 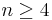 it is simply-connected and has the integral cohomology structure of the complex projective plane
it is simply-connected and has the integral cohomology structure of the complex projective plane 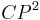 (
(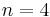 ), of the quaternionic projective plane
), of the quaternionic projective plane 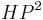 (
(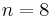 ) or of the Cayley projective plane (n = 16).
) or of the Cayley projective plane (n = 16).
Properties
These manifolds are important in both Morse theory and foliation theory:
Theorem:[1] Let  be a connected closed manifold (not necessarily orientable) of dimension
be a connected closed manifold (not necessarily orientable) of dimension  . Suppose
. Suppose  admits a Morse function
admits a Morse function 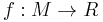 of class
of class 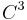 with exactly three singular points. Then
with exactly three singular points. Then  is a Eells–Kuiper manifold.
is a Eells–Kuiper manifold.
Theorem:[2] Let 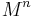 be a compact connected manifold and
be a compact connected manifold and  a Morse foliation on
a Morse foliation on  . Suppose the number of centers
. Suppose the number of centers  of the foliation
of the foliation  is more than the number of saddles
is more than the number of saddles  . Then there are two possibilities:
. Then there are two possibilities:
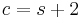 , and
, and 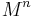 is homeomorphic to the sphere
is homeomorphic to the sphere 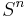 ,
,
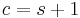 , and
, and 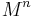 is an Eells—Kuiper manifold,
is an Eells—Kuiper manifold, 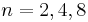 or
or 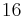 .
.